The 2025 Soifer Mathematical Olympiad
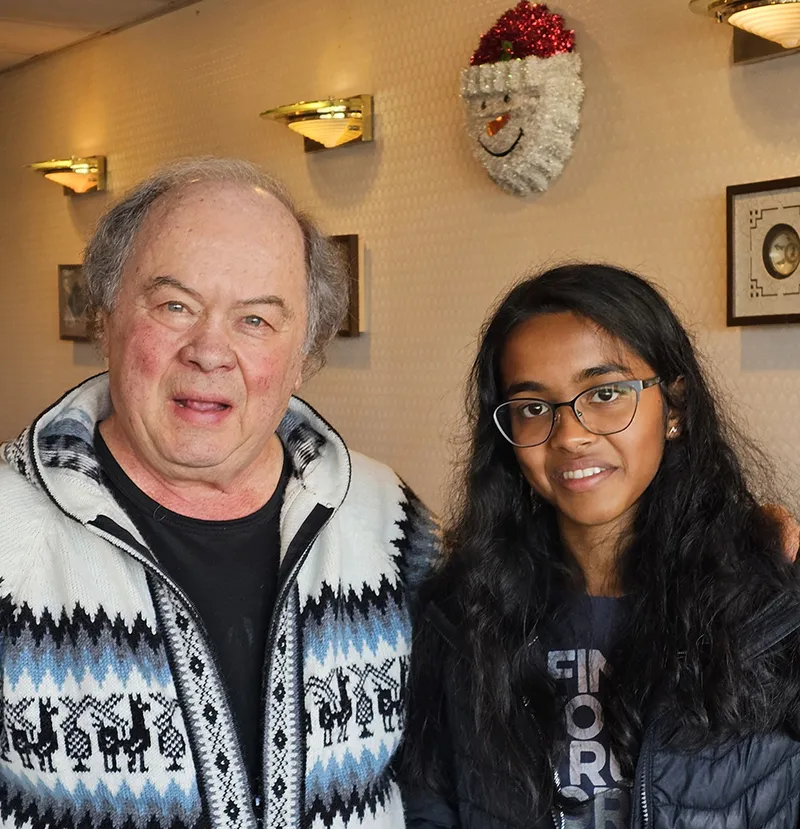
The 41st Soifer Mathematical Olympiad will be held on October 3, 2025. The Awards Ceremony will be held on October 10, 2025.
Parking will be free for the event on both days on the UCCS campus in lots 220, 222 and 224. For more information, see the
(2025 Event Flyer).
Left: Dr. Alexander Soifer and Soifer Mathematical Olympiad gold, silver and bronze medalist, Shruti Arun.
40th Soifer Mathematical Olympiad October 4, 2024

Brother and sister Arun impress jury of 39th Soifer Mathematical Olympiad

135 Olympians came from all over Colorado to compete in the 39th Soifer Mathematical Olympiad on October 6. Participants were from Aurora, Broomfield, Centennial, Cherry Hills Village, Colorado Springs, Denver, Englewood, Fountain, Greeley, Greenwood Village, Highlands Ranch, Littleton, Lone Tree, Loveland, Snowmass Village, Timnath, Windsor and Woodland Park.
38th Soifer Mathematical Olympiad
Mind Games at UCCS; Olympians conquer Olympiad
On October 7, 2022 over 150 Olympians came from all over Colorado to participate in the 38th Soifer Mathematical Olympiad.
More Information
Donate- Contribute
To support the Soifer Mathematical Olympiad Program at the University of Colorado Colorado Springs, follow these steps:
- Click the link below.
- Under "Gift Designations," select "Other."
- In the provided text box, write "Math Olympics Support Fund."
Register
Registration for the 41st Soifer Mathematical Olympiad will begin on March 1, 2025. Please check back! Thank you!
